crosthebest.blogg.se - Geometer sketchpad lessons

#Geometer sketchpad lessons how to
#Geometer sketchpad lessons series

Particularly for transformational proofs, such figures can be clearer and more convincing in a dynamic environment that supports animating the transformation.

#Geometer sketchpad lessons series

Proofs Without Words is a series of books from the American Mathematical Society containing “figures or diagrams that help the reader see why a particular mathematical statement may be true and how one could begin to go about proving it.” Though the figures themselves are not technically proofs, they are elegant graphical illustrations of the important mathematical truths whose proofs they suggest. Take a look at both activities, and for each activity predict several things that students might say to explain why one is different from the other three.

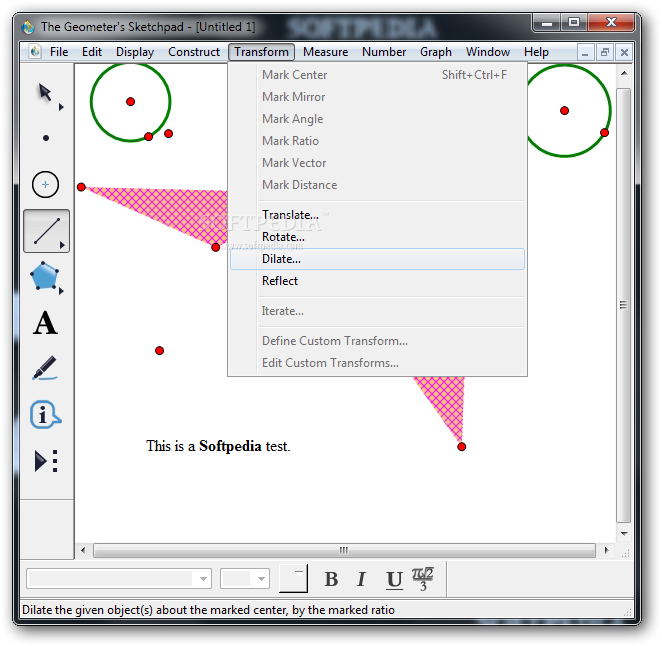
Next, let's compare two WODB student activities, one based on Cartesian graphs and one based on Dynagraphs. Since you already know that dilation corresponds to multiplication, and translation to addition, what kind of algebraic function is created by the composition `T(D(x))?` Source: This activity comes from the lesson Construct a Dynagraph. Write a formula for the value of `T(D(x))` in terms of `x, s,` and `v.` Check your formula by varying `x` and adjusting `s` and `v.`.Use pages 2 and 3 to construct more functions, and to show how different values of `s` and `v` affect the shape of the traces.How can you tell from the traces whether `T(D(x))` is moving in the same direction or the opposite direction as `x?` Draw pictures to support your explanation.Try different values of `s` and `v.` How can you tell from the traces whether `T(D(x))` is moving faster or slower than `x?` Draw pictures of your traces to explain your answer.

When you vary `x,` what do you notice about the traces of the connecting line?.Connect `x` on the top number line to `T(D(x))` on the bottom line, and use the Trace Widget to turn tracing on for the connecting line.As you vary `x`, how is the value of `T(D(x))` related to `D(x)` and `v?` Write both a description and a formula.Translate the new `D(x)` on its number line.Then use the Visibility Widget to hide the dashed lines. Vary `x` to make sure the two `D(x)` variables always match.Transfer both the origin and `D(x)` downward, and construct a new number line matching its origin to the transferred origin.As you vary `x`, how is the value of `D(x)` related to `x` and `s?` Write both a description and a formula.Construct `D(x)` with `x` restricted to a number line.As you work, practice the different ways of placing the given objects of the tools. Use the tools in the sketch below to construct a triangle and its orthocenter.

#Geometer sketchpad lessons how to

After checking out the tool’s effect, tap the Undo arrow to undo.īecause all tools work this same way, it’s easy for you and your students to figure out how to use them with no need for additional documentation, explanation, or demonstration.

To preview the results of any tool, choose it and then tap the green OK button.

Until the tool is finished, you can drag any already-matched given object to reposition or rematch it.

drag any given object, whether it’s glowing or not.

Tap to position or match the glowing object, or.

Everything the tool will produce is immediately visible, with the first object to be matched already glowing.

I think this was a very effective way to help students generate and understand the Pythagorean Theorem. Lastly, it has the students construct a non-right triangle and show that the theorem only holds true for right triangles. Although the measurements change, the relationship remains the same. It has the students drag one of the vertices of the triangle and examine how the relationships between the side lengths and their squares change. Next, the activity makes use the of the dynamic features of Sketchpad. At this point the students see the relationship that the sum of the squares of the legs is equal to the square of the hypotenuse. Next though, the activity has them square each of the measurement and add the squares of the legs together. At this point there shouldn’t really be anything that jumps out at the students. After this, the activity has the students calculate the measurements of the side lengths of the triangle. It is good that the activity stresses this so that the students know that the triangle has a 90 degree angle in it. The first step of this is to construct the two perpendicular legs of the triangle. First, it has the students go through the process of constructing a right triangle. This sketchpad activity is the one that we did during class, and it explores how we come up with the Pythagorean Theorem.